Kunci Jawaban Matematika Uji Kompetensi halaman 102 kelas 9

beritawarganet.com – Kunci Jawaban Matematika Uji Kompetensi halaman 102 kelas 9. Pada mata pelajaran matematika kelas Sobat BW akan mendapat materi tentang sumbu simetri dan titik optimum.

Kali ini, beritawarganet akan membahas kunci jawaban matematika Soal latihan 2.3 Bab sumbu simetri. Pertanyaan ini bisa sobat BW temukan pada buku matematika kurikulum 2013 kelas 9 halaman 102.

Pembahasan berikut bisa sobat BW simak untuk mencocokan dengan jawaban yang telah sobat BW kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya!

Kunci Jawaban Matematika Uji Kompetensi halaman 102 kelas 9

1. Tentukan sumbu simetri grafik fungsi di bawah ini.

a. y = 2x² − 5x
b. y = 3x² + 12x
c. y = –8x² − 16x − 1

Jawaban :

a) Sumbu simetrinya adalah x = -b/2a = – (-5 / 2×2) = 5/4
b) Sumbu simetrinya adalah x = -b/2a = – (12 / 2×3) = -2
c) Sumbu simetrinya adalah x = -b/2a = – (-16 / 2x(-8)) = -1

2. Tentukan nilai optimum fungsi berikut ini.

a. y = –6x² + 24x − 19
b. y = 25 x² – 3x + 15
c. y = 34 − x² + 7x − 18

Jawaban :

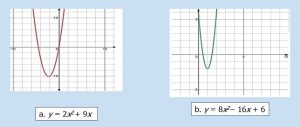
3. Sketsalah grafik fungsi berikut ini.

a. y = 2x² + 9x
b. y = 8x² − 16x + 6

Jawaban :

 

4. Diketahui suatu barisan 1, 7, 16, …. Suku ke-n dari barisan tersebut dapat dihitung dengan rumus Un = an2 + bn + c. Tentukan suku ke 100.

Jawaban :

5. Diketahui suatu barisan 0, –9, –12, …. Suku ke-n dari barisan tersebut dapat dihitung dengan rumus Un = an2 + bn + c. Tentukan nilai minimum dari barisan tersebut.

Jawaban :

6. Fungsi kuadrat y = f(x) melalui titik (3, –12) dan (7, 36). Jika sumbu simetrinya x = 3, tentukan nilai minimum fungsi f(x).

Jawaban :

7. Bila fungsi y = 2×2 + 6x − m mempunyai nilai minimum 3 maka tentukan m.

Jawaban :

Sumbu simetrinya adalah x = -b / 2a = – 6 / (2×2) = -6/4 ,
subtitusi nilai x kedalam fungsi y
2(-6/4)2 + 6(-6/4) – m = 3
m = 2(36/16) – 9 – 3

m = -15/2

Jadi, nilai m adalah -15/2.

8. Dari tahun 1995 sampai 2002, banyaknya pelanggan telepon genggam N (dalam juta orang) dapat dimodelkan oleh persamaan N = 17,4×2 + 36,1x + 83,3, dengan x = 0 merepresentasikan tahun 1995. Pada tahun berapa banyaknya pelanggan mencapai nilai maksimum?

Jawaban :

Dilihat dari persamaan N, nilai N akan selalu lebih besar apabila x + 1 > x.
1995 nilai x = 0
1996 nilai x = 1
1997 nilai x = 2
2002 nilai x = 7

Sehingga pelanggan maksimum akan terjadi pada tahun 2002 dengan x = 7, subtitusi x ke persamaan N

N = 17,4×2 + 36,1x + 83,3
= 17,4(7)2 + 36,1(7) + 83,3
= 1,1886 miliar pengguna

Jadi banyak pelanggan mencapai nilai maksimum terjadi pada tahun 2002 dengan jumlah pelanggan 1,1886 miliar pengguna.

9. Jumlah dua bilangan adalah 30. Jika hasil kali kedua bilangan menghasilkan nilai yang maksimum, tentukan kedua bilangan tersebut.

Jawaban :

Misalkan dua bilangan tersebut adalah a, b dan = 30 – b

f(b) = a × b = (30 – b) × b = 30b – b2
nilai turunan = 0
30 – 2b = 0
2b = 30
b = 15

a = 30 – b
a = 30 – 15 ; a = 15

Jadi, nilai kedua bilangan tersebut adalah 15 dan 15.

10. Selisih dua bilangan adalah 10. Jika hasil kali kedua bilangan menghasilkan nilai yang minimum, tentukan kedua bilangan tersebut.

Jawaban :

Misalkan dua bilangan tersebut adalah a, b dengan a > b maka a = 10 + b sehingga

f(b) = a × b = (10 + b) × b = 10b + b2
nilai turunan = 0
10 + 2b = 0
2b = -10
b = -5

a = 10 + b
a = 10 – 5 ; a = 5

Jadi, nilai kedua bilangan tersebut adalah -5 dan 5.

 

 

Disclaimer:

1. Kunci jawaban pada unggahan BW tidak mutlak kebenarannya
2. Unggahan ini bisa sobat BW gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Kunci jawaban pada unggahan BW mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

Penutup

Sekian penjelasan yang bisa BW bagikan. Jangan lupa simak pembahasan-pembahasan lainnya pada unggahan BW yang lain ya sob!

Semoga bermanfaat